Look Forward, Reason Backward: A Primary Principle of Strategic Thinking

One of the basic principles in game theory is that you should look forward and reason back.

Essentially, this means that before making a move, you should consider all the possible moves that you and the other players can make, together with the possible outcomes that these moves lead to. Then, consider how desirable each outcome is to each player, and based on this, determine which moves other players are likely to make, and which move you should make yourself.

In the following article, you will see how the principle of look forward and reason backward works, and how you can implement it in order to make smarter decisions.

Example: to advertise or not to advertise?

Consider the following scenario:

MegaCorp is currently the only company selling a certain type of high-quality industrial lasers.

Startupo is a new company, which is considering entering the market currently dominated by MegaCorp.

To deter Startupo from competing against them, MegaCorp can engage in a costly advertising campaign, which would involve significantly reducing their profits.

Since Startupo is a smaller and more flexible company, they can wait and see whether MegaCorp runs their ad campaign before deciding whether they should enter the market.

As such, each company has two possible moves: MegaCorp can decide whether or not to run the ads, while Startupo can decide whether or not to enter the market.

This means that there are 4 possible outcomes for this scenario, each of which is ranked differently by the players, with ‘1’ being the most desirable outcome, and ‘4’ being the least desirable outcome:

Megacorp’s outcome ranking:

1. No ads, no entry (of Startupo).
2. Ads, but no entry.
3. No ads, but entry.
4. Ads and entry.

Startupo’s outcome ranking:

1. No ads, yes entry.
2. Ads, but no entry.
3. No ads and no entry.
4. Ads and entry.

Based on this, we get the following game tree (also known as a decision tree in cases where there is only one player), which illustrates all the possible moves and outcomes in this scenario:

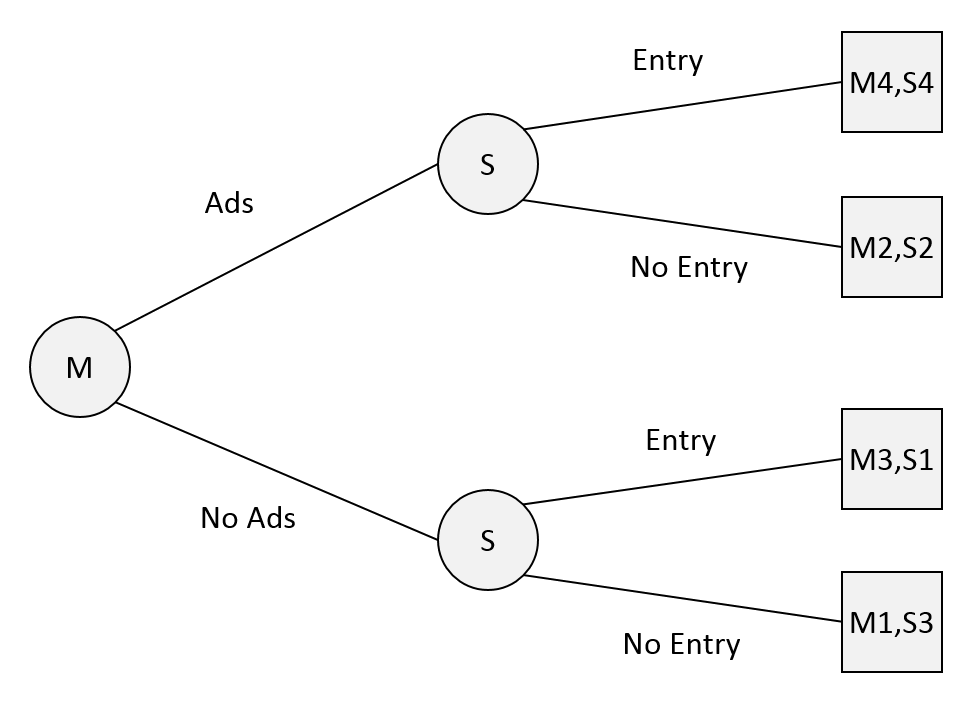
Essentially, when making the decision whether to or not advertise, MegaCorp starts by looking at all the possible outcomes of this scenario, and then asking themselves which moves their competitor is most likely to make:

• If MegaCorp runs the ads, then Startupo will choose not to enter the market, since doing this gets them their #2 outcome, as opposed to their #4 outcome. This choice means that MegaCorp also gets their #2 outcome.
• If MegaCorp doesn’t run the ads, then Startupo will likely choose to enter the market, since it leads to a better outcome for them than not entering the market (outcome #1 versus outcome #3). In this case, MegaCorp will get their #3 outcome.

Based on this, it’s clear that MegaCorp should run its advertising campaign, in order to prevent Startupo from entering the market. Doing this means that they will get their #2 choice, similarly to Startupo, while if they decide to not run the ads, then they will get their #3 choice, while Startupo will get their #1 choice.

Here, we applied the principle of looking forward and reasoning backward by first considering the possible outcomes of the scenario, and then working our way back in order to figure out all the possible countermoves that Startupo can make in response to Megacorp, in order to figure out the best course of action for Megacorp.

Considerations when applying this principle

This method of backward induction can be used in order to find the optimal solution of a game when the following conditions apply:

• Sequentiality: the game must be sequential, meaning that the players act one after another (as opposed to a simultaneous game, where the players act at the same time).
• Finiteness: the game must be finite, meaning that it must have a clear endpoint.
• Perfect information: the players must have perfect information regarding the possible moves and outcomes of the game, as well as regarding the desirability of each outcome.
• Rationality: all players must choose their move rationally, meaning that they must select the option that is best for them.

Of course, in reality, things are complicated, and these conditions may not all be satisfied, especially since perfect information rarely exists, and since people often tend to make irrational decisions. This is further complicated by the fact that games can have more than just two players, each of which can often have multiple possible moves, and various complex motives.

This all leads to an important caveat: just because the game has an optimal strategy that you should select, doesn’t mean that it’s easy to find it (chess is a good example of this). However, these extra factors and considerations can be often be incorporated into the model, and backward induction nevertheless remains the best way to deal with many of these scenarios, which are going to be complex regardless of how you approach them.

Summary and conclusions

• The principle of looking forward and reasoning backward represents the concept of backward induction, which is the idea that you should start reasoning backward from the end of a problem, in order to identify your optimal course of action.
• Essentially, this means that before making a move, you should consider the possible moves that you and the other players can make, together with the possible outcomes that these moves will lead to. Then, rank the different outcomes in terms of their desirability for each player, and based on this, determine which moves other players are likely to make.
• In order to illustrate all of this in a clear way, you should use a game tree, which maps the possible moves that each player can make, and the outcomes that these moves will lead to. Once you have the full game tree mapped out, you can reason backward in order to identify the optimal moves for you to make.
• There are some conditions that must apply in order for this strategy to work. These include having the players take turns in a sequential way, having a set endpoint for the “game”, having perfect information available for all the players, and having the players make perfectly rational decisions.
• Applying this strategy can be difficult in real life, where scenarios are often complex, and where some of the necessary conditions may not exist. However, backward induction is still one of the best ways to handle many of these scenarios, which are going to be difficult to solve regardless of which method you use.

The rationale behind this strategy and its example comes from “The Art of Strategy: A Game Theorist’s Guide to Success in Business and Life“. It’s a good read for someone looking to understand basic game theory and how it applies to real-life situations.