
The law of small numbers is the incorrect belief that small samples are likely to be highly representative of the populations they come from (similarly to large samples).
For example, the law of small numbers could cause someone to assume that the way one person behaves necessarily represents the way everyone from that person’s country behaves.
The law of small numbers, which is sometimes also referred to as the LOSN effect or LSN, can strongly influence people’s thinking in a variety of domains, so it’s important to understand it. As such, in the following article you will learn more about the law of small numbers, and see how you can account for it in practice.
Examples of the law of small numbers
An example of belief in the law of small numbers is someone who draws generalizations about an entire group of people, such as those with a shared gender, nationality, or religion, based on the behavior of one of its members, even though the behavior of the individual member may not be representative of the behavior of other group members.
Another example of the law of small numbers, this time in a medical context, is someone who assumes that if a certain symptom is known to occur in around half of the patients that suffer from a certain condition, then in a group of 4 patients exactly 2 of them (i.e., exactly half) will necessarily have that symptom, even though it is possible and likely that a different number of them will have that symptom, due to the random variability involved.
In addition, studies in the fields of psychology and behavioral economics have found evidence of belief in the law of small numbers among various samples, including students, entrepreneurs, investors, economists, and even professional psychologists, who displayed this belief in various domains. For example, one study states the following about the law of small numbers in the context of financial decisions:
“The law of small numbers… not only reconciles gambling behavior and betting in sports markets, but may also provide a unifying framework to account for several anomalies observed in financial markets.
One of these anomalies is that asset prices underreact to news in the short run and overreact over long time horizons. In a nutshell, the reasoning is as follows. If many investors… believe that short sequences of unexpectedly high earnings will quickly reverse in the future, stock prices will underreact to news about earnings. The same investors, if uncertain about the process behind earnings sequences, attribute long streaks of unexpectedly high earnings to an underlying fundamental and expect such streaks to continue, leading to overreaction of stock prices in the long run… Among investors who are confident that earnings are i.i.d. [independent and identically distributed], underreaction persists and may even become stronger, the longer the streak.”
—From “Predicting Lotto Numbers: A Natural Experiment on the Gambler’s Fallacy and the Hot-Hand Fallacy” (Suetens, Galbo-Jørgensen, & Tyran, 2016)
Furthermore, a different study gives examples of how a scientist might be affected by their belief in the law of small numbers:
“Consider a hypothetical scientist who lives by the law of small numbers. How would his belief affect his scientific work? Assume our scientist studies phenomena whose magnitude is small relative to uncontrolled variability, that is, the signal-to-noise ratio in the messages he receives from nature is low. Our scientist could be a meteorologist, a pharmacologist, or perhaps a psychologist…
…the believer in the law of small numbers practices science as follows:
- He gambles his research hypotheses on small samples without realizing that the odds against him are unreasonably high. He overestimates power.
- He has undue confidence in early trends (e.g., the data of the first few subjects) and in the stability of observed patterns (e.g., the number and identity of significant results). He overestimates significance.
- In evaluating replications, his or others’, he has unreasonably high expectations about the replicability of significant results. He underestimates the breadth of confidence intervals.
- He rarely attributes a deviation of results from expectations to sampling variability, because he finds a causal ‘explanation’ for any discrepancy. Thus, he has little opportunity to recognize sampling variation in action. His belief in the law of small numbers, therefore, will forever remain intact.”
— From “Belief in the law of small numbers” (Tversky & Kahneman, 1971)
Finally, another study gives additional examples of how belief in the law of small numbers can influence scientists:
“The believer in the law of small numbers habitually overestimates the amount of information about the population contained in small samples and the power of statistical analysis to extract that information.
As a result, he frequently employs small samples in his research, samples that can under no circumstances answer the questions put to them. Then when such research produces results inconsistent with predictions, as it must for statistical reasons alone, additional ‘explanatory variables’—often moderators—are hypothesized to account for what in actuality was produced by statistical artifacts.”
— From “Moderator research and the law of small numbers” (Schmidt & Hunter, 1978)
Consequences of the law of small numbers
The consequences of people’s belief in the law of small numbers manifest in several main ways:
- Biased perception and prediction of small samples. This involves assuming that small samples are representative of their parent populations, or expecting future small samples to be representative. For example, this can involve assuming that the behavior of a single person from a certain country is highly representative of the behavior of everyone from that country, or expecting a person from a certain country to act exactly in accordance with the stereotypes associated with people from that country.
- Biased perception and prediction of large samples. This involves assuming that if a large sample is not locally representative then it’s not random, or expecting future large samples to be locally representative if they’re drawn or generated in a random manner. For example, this can cause someone to assume that if a series of 100 coin-tosses has a sequence of 5 heads in a row then it’s not random, or to assume that a random series of 100 coin-tosses won’t contain any such sequences.
Based on these types of consequences, it’s possible to categorize the law of small numbers as perceptive in cases where it influences people’s perceptions and assessment of samples, and as predictive, in cases where it influences people’s predictions of samples. In addition, it is also possible to distinguish between cases where the law of small numbers influences people’s perception/prediction of small samples and those where it influences people’s perception/prediction of large samples.
Finally, note that the above consequences can also lead to related issues, such as biased generation of data. For example, when people are asked to simulate a random process, they tend to produce sequences that are locally representative, contrary to the type of data that would be generated by a truly random process. In the case of a coin toss, for instance, this can mean that they will generate a sequence with too many alternations and too few clusters (e.g., no cases of the coin landing on heads 3 times or more in a row).
The psychology and causes of the law of small numbers
The law of small numbers can be characterized as a cognitive bias that involves the incorrect expectation of local representativeness, in the sense that people expect small samples to be fully representative of the characteristics of the parent population from which they are drawn, similarly to large samples. Essentially, this means that people expect the characteristics of the population to be represented not only globally in the entire population (or in large samples), but also locally in all of its parts.
This pattern of thinking is sometimes viewed as a potentially beneficial heuristic, which is a mental shortcut that can help people judge information and make decisions quickly, especially under uncertainty, but which can also lead them to make erroneous judgments. For example, as one study notes:
“Throughout our evolutionary history, it is likely that humans confronted minimally-sized samples exclusively, for which our current limited-capacity numerical cognition served us adequately… The numerical representations we seem hardwired to invoke are ill-suited for the processing of large samples. Dehaene et al. propose that we have, in essence, a very precise number-sense for reasoning about very small quantities (~4), and a separate modality—blurred and less precise— that we apply to large quantities… Evidently, our limited working memory and numerical cognition systems have historically been sufficient for our persistence as a species, and a more sophisticated reasoning apparatus was never selected for…
Prejudices are exemplary of how the use of minimal information to reach far-fetched conclusions may make sense… With respect to decision making in the natural world, such generalizations lead to favorable outcomes more often than decisions left up to chance. Furthermore, a strong proclivity toward over-generalization is probably—or once was—critical to survival. If this morning I witnessed a fellow human enter a cave and subsequently get eaten by a bear, it is likely in my interests to be particularly cautious about entering into new caves from now on…
…the law of small numbers is likely not the best possible performing strategy with respect to inferential accuracy, but it is saliently conservative in resource utilization, and necessitates very little information to function, as compared to other more sophisticated systems. And in an environment where a great deal of observable events have appreciable underlying causes, a generally rapid-trigger inductive system could be not only good enough, but even a superior alternative to time and resource consuming systems…
In forming our causal accounts of phenomena, however, we tend to overlook the role of chance—the unexplainable variation or noise that pervades our acquired data. The survival of a particular tribe does not depend on the numeric average of an infinite ideal population, but rather on the hunters returning to the village with meat. And we all know that to arrive at the average necessitates our surrendering at least some of the details that give sense to the world. Human survival profoundly hinges on an uncanny ability to decipher sensible patterns amidst an overwhelming flux of peripheral stimuli, in practice ignoring the chance part of the equation. Although it is an unavoidable truth that we often make mistakes, the fact that we continue to stick around might be living proof that we are right more often than not; so, perhaps the law of small numbers is not so bad after all.”
— From “Small samples and evolution: did the law of small numbers arise as an adaptation to environmental challenges?” (Navarrete, Santamaría, & Froimovitch, 2015). However, note that the authors themselves state that this kind of evolutionary argument should be treated with caution.
In addition, Daniel Kahneman, one of the two researchers who first identified this phenomenon in the early 1970s, also said the following about it, several decades later:
“Thanks to recent advances in cognitive psychology, we can now see clearly what Amos and I could only glimpse: the law of small numbers is part of two larger stories about the workings of the mind.
- The exaggerated faith in small samples is only one example of a more general illusion—we pay more attention to the content of messages than to information about their reliability, and as a result end up with a view of the world around us that is simpler and more coherent than the data justify. Jumping to conclusions is a safer sport in the world of our imagination than it is in reality.
- Statistics produce many observations that appear to beg for causal explanations but do not lend themselves to such explanations. Many facts of the world are due to chance, including accidents of sampling. Causal explanations of chance events are inevitably wrong.”
— From “Thinking, Fast and Slow“ (Kahneman, 2011)
Finally, various factors can influence the likelihood that people will display belief in the law of small numbers in different circumstances. For example, when it comes to drawing generalizations about group members from the behavior of one of its members, people are more likely to display belief in the law of small numbers with regard to people who are not part of their social group (i.e., people who are in their outgroup, rather than their ingroup).
Association with the law of large numbers
The law of small numbers can be understood in relation to the law of large numbers, which is a concept in probability theory that denotes that as the size of a sample increases, the sample will generally become more representative of the population from which it is drawn, especially initially. This law means, for example, that in the case of a fair coin toss, the ratio between heads and tails is more likely to be close to 1:1 in a series of 100 coin tosses than in a series of 10 tosses. As one work on the topic notes:
“The Law of Large Numbers states that larger samples provide better estimates of a population’s parameters than do smaller samples. As the size of a sample increases, the sample statistics approach the value of the population parameters. In its simplest form, the Law of Large Numbers is sometimes stated as the idea that bigger samples are better.”
— From “Law of Large Numbers” in the Encyclopedia of Research Design (2012)
The difference between the law of large numbers and the law of small numbers is that the law of large numbers is a statistical concept, whereas the law of small numbers is a psychological concept, and while these concepts are associated with one another, they refer to different phenomena. Specifically, the law of large numbers denotes that as the size of a sample increases, it will generally become more representative of the population from which it is drawn, while the law of small numbers is the incorrect belief that small samples are likely to be highly representative of the populations from which they are drawn, similarly to large samples.
Accordingly, the law of small numbers can be viewed as the belief that the law of large numbers applies to small samples too, in the sense that people mistakenly assume that small samples are as representative of their parent population as large samples are.
This distinction is illustrated, for example, in the case of a coin toss, where the law of small numbers involves the mistaken belief that short sequences of tosses will be highly representative of long sequences of tosses. For instance, if a coin has a 50% chance of landing on either side, then someone who believes in the law of small numbers will mistakenly expect the coin to almost always land equally on heads and tails, even when the coin is tossed only a small number of times. However, this is not the case, as shown in the following diagram.
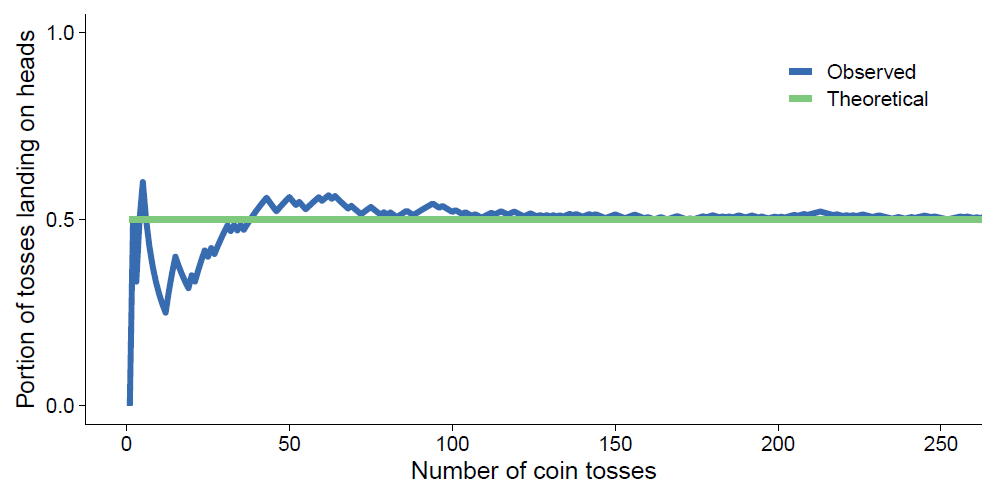
The same principle also applies in situations other than coin tosses. For example, consider a situation where you want to measure a certain trait in the population, for which the average (i.e., mean) value in the population is 5 (on a scale of 1–10). If you start with a small sample, of only 3 people, you might get an average of 7 in the sample, due to chance. As you increase the sample size, you can expect the observed average of the sample to become closer to the population average, especially initially. This means that if you increase the sample to 50 people, it might go to 5.5, and if you increase it to 100 people, it might go to 5.1. However, people who display belief in the law of small numbers might assume that the initial sample, of only 3 people, is enough to accurately determine the true average of the entire population.
Note: there is more to the law of large numbers, for example when it comes to convergence and the difference between the weak and strong laws of large numbers. However, these distinctions are not crucial when it comes to understanding this concept in the context of the law of small numbers.
How to reduce your own belief in the law of small numbers
There are several things that you can do to reduce your belief in the law of small numbers.
First, you should understand what the law of small numbers is, why it’s problematic, and when and how it can influence your thinking.
Second, you should identify specific situations where you might be displaying belief in the law of small numbers, or have done so in the past or will do so in the future. To identify such cases, and to reduce the bias that you display in them, you can clearly and explicitly outline your associated reasoning (e.g., explain why you think that a certain sample should look a certain way), and actively question your reasoning (e.g., by asking “is a sample of one person really enough to draw meaningful conclusions?”).
When doing this, you can also ask yourself additional guiding questions, such as how certain you are of your assessment, or how you would feel about inferring, based on a similar sample, a similar conclusion that contradicts your pre-existing beliefs. Furthermore, you can use various additional debiasing techniques, such as slowing down your reasoning process, improving your decision-making environment, considering alternative hypotheses, and using self-distanced language (e.g., by asking yourself “why do you think that this sample is large enough?” instead of “why do I think that this sample is large enough?”).
Finally, in some contexts, such as in finance or in scientific research, it may be possible to determine whether a certain sample is large enough to be considered representative of its parent population by using appropriate statistical measures, such as statistical power and statistical significance. In addition, in such situations and in others, you may also be able to approximate how large a sample needs to be in order to be reasonably representative of its parent population, based on things such as prior experience.
When doing this, keep in mind that the size of a sample (e.g., number of people or number of coin tosses) isn’t the only thing that matters to your assessment. Rather, other factors, such as the following, can also play an important role:
- Effect size. For example, when it comes to measuring how much a certain intervention helps people, the more helpful the intervention is, the greater the effect size involved. Smaller effect sizes generally make it more difficult to infer things about the parent population based on a small sample.
- Variability. For example, when it comes to measuring a certain personality trait in a group of people, high variability roughly means that individuals tend to have very different values for that trait. Greater variability generally makes it more difficult to infer things about the parent population based on a small sample.
Overall, to reduce your own belief in the law of small numbers, you should understand the causes and consequences of this bias, identify situations where you might display it, and address it with relevant debiasing techniques, such as making your reasoning explicit and questioning it (e.g., by asking if a sample is large enough to draw conclusions about its parent population). You can potentially also consider other relevant factors, such as the variability within the population (since greater variability generally makes it harder to draw inferences about small samples).
How to reduce other people’s belief in the law of small numbers
There are several things that you can do to reduce people’s belief in the law of small numbers, which are similar to the things that you can do to reduce your own belief in the law of small numbers yourself.
First, you can explain to them what this concept is, why it’s problematic, when it can occur, and how it can influence people’s thinking. When doing this, you can use specific examples to illustrate this concept and its associated issues, and preferably examples that are related to your present circumstances. In addition, you can also explain associated concepts, such as variability and the law of large numbers, which may play a role in situations where people display belief in the law of small numbers.
You can also ask the other person if they think that they might be displaying this belief, and if not, then what makes them think that they aren’t. When doing this, you can encourage them to make their reasoning explicit, in order to make it easier to identify any issues with it. You can also ask them various questions to help them guide their reasoning, such as “how likely is it that a single random person is perfectly representative of their entire social group?”.
Furthermore, if you see evidence that they are in fact displaying belief in the law of small numbers, you can ask them about this evidence or point it out to them directly. In addition, you can also present them with relevant examples that illustrate the problem with their way of thinking. For example, if they’re making overgeneralizations about groups of people based on the behavior of a single individual, you can ask them how they would feel if someone did something similar to them.
Finally, you can also help or encourage them to use relevant debiasing techniques, such as slowing down their reasoning process and improving the decision-making environment.
However, note that in some cases, there may be nothing that you can do to prevent someone from displaying this bias, or from displaying other biases that are caused by this, such as jumping to conclusions and overgeneralizing from anecdotal evidence and small samples. Nevertheless, it can still be beneficial to understand how this bias influences people’s thinking in such cases, because this can help you understand people’s motives and rationale, and can consequently help you predict their behavior and find solutions to their bias-driven behaviors.
Overall, to reduce other people’s belief in the law of small numbers, you can explain to them what this concept is and illustrate it with relevant examples, ask them whether they could be displaying it, question or point out issues with their reasoning, and encourage them to use general debiasing techniques, such as slowing down their reasoning process.
Additional information
The origin of the law of small numbers
The concept of the law of small numbers, in the context discussed here, was first outlined by researchers Amos Tversky and Daniel Kahneman in their 1971 paper titled “Belief in the law of small numbers”, where they state the following:
“People have erroneous intuitions about the laws of chance. In particular, they regard a sample randomly drawn from a population as highly representative, that is, similar to the population in all essential characteristics. The prevalence of the belief and its unfortunate consequences for psychological research are illustrated by the responses of professional psychologists to a questionnaire concerning research decisions…
We submit that people view a sample randomly drawn from a population as highly representative, that is, similar to the population in all essential characteristics. Consequently, they expect any two samples drawn from a particular population to be more similar to one another and to the population than sampling theory predicts, at least for small samples.
The tendency to regard a sample as a representation is manifest in a wide variety of situations. When subjects are instructed to generate a random sequence of hypothetical tosses of a fair coin, for example, they produce sequences where the proportion of heads in any short segment stays far closer to than the laws of chance would predict (Tune, 1964). Thus, each segment of the response sequence is highly representative of the ‘fairness’ of the coin. Similar effects are observed when subjects successively predict events in a randomly generated series, as in probability learning experiments (Estes, 1964) or in other sequential games of chance. Subjects act as if every segment of the random sequence must reflect the true proportion: if the sequence has strayed from the population proportion, a corrective bias in the other direction is expected. This has been called the gambler’s fallacy…
Thus far, we have attempted to describe two related intuitions about chance. We proposed a representation hypothesis according to which people believe samples to be very similar to one another and to the population from which they are drawn. We also suggested that people believe sampling to be a self-correcting process. The two beliefs lead to the same consequences. Both generate expectations about characteristics of samples, and the variability of these expectations is less than the true variability, at least for small samples.
The law of large numbers guarantees that very large samples will indeed be highly representative of the population from which they are drawn. If, in addition, a self-corrective tendency is at work, then small samples should also be highly representative and similar to one another. People’s intuitions about random sampling appear to satisfy the law of small numbers, which asserts that the law of large numbers applies to small numbers as well.”
— From “Belief in the law of small numbers” (Tversky & Kahneman, 1971)
Related psychological phenomena
There are many psychological phenomena that are closely related to the law of small numbers.
One such phenomenon is the representativeness heuristic, which is the tendency to evaluate probabilities by the degree to which one thing is representative of another. This means that the probability of something such as an event or a sample may be evaluated by the degree to which it is similar in its essential properties to its parent population, or by the degree to which it reflects the salient features of the process that generated it.
Another related phenomenon is jumping to conclusions, which occurs when people reach a conclusion prematurely, on the basis of insufficient information. A notable way of jumping to conclusions, which is particularly associated with the law of small numbers, is overgeneralization (also referred to in some cases as hasty generalization), which involves taking a piece of information that applies to specific cases and then applying it in other, more general cases, in an unreasonable manner.
In addition, two other phenomena that are closely related to the law of small numbers and to each other, are the gambler’s fallacy and the hot-hand fallacy. Specifically, the gambler’s fallacy is the mistaken belief that if an event occurred more frequently than expected in the past then it’s less likely to occur in the future (and vice versa), in a situation where these occurrences are independent of one another. Conversely, the hot-hand fallacy is the mistaken belief that a string of similar outcomes signals that additional similar outcomes are likely to follow, in a situation where these outcomes are independent of one another.
Finally, the law of small numbers is associated with a number of related phenomena, such as the tendency to view chance as a fair process, the availability heuristic, which represents people’s tendency to rely more strongly on information that is easy for them to bring to mind, and the insensitivity to sample size phenomenon (also known as sample-size neglect), whereby people fail to consider sample size when making judgments about probability.
Related mathematical concepts
Outside the context of psychology and behavioral economics, the term “law of small numbers” is also used with a different meaning in the context of mathematics and probability. As one paper notes:
“The meaning of the ‘Law of Small Numbers’ has been the subject of widespread misapprehension, to the extent that there has been a convergent tendency to interpret it as the Poisson probability distribution, in the sense that this distribution describes the occurrence of rare events in the setting of binomial trials. This was not Bortkiewicz’s understanding of the LSN, although the Poisson distribution plays a very prominent role in the setting in which the term ‘Law of Small Numbers’ first appears (Bortkewitsch, 1898), and within the real-life examples in this work, among which is the horse kick data, by which Bortkiewicz illustrated his understanding of the LSN…
[The LSN] asserts that relatively short series of N independent observations, each on a Poisson (λj) (j = 1,… , N) distribution, tend to behave as if they are a sample of size N from a (homogeneous) Poisson distribution even if the λj‘s are unequal. In the case of unequal λj‘s the larger the ‘scale of experience’, the more readily can the heterogeneity among the λj‘s be detected…”
— From “Bortkiewicz’s Data and the Law of Small Numbers” (Quine & Seneta, in the International Statistical Review / Revue Internationale de Statistique, 1987)
In addition, this term has been used in a number of other, more niche ways.
For example, an initial version of a research paper used this term when discussing a phenomenon whereby “small price markets exhibit greater mispricing than large price markets”, which was attributed to “the co-existence of two mental scales, a linear one for small numbers and a logarithmic one for large numbers”. However, a later version of the same paper avoided the use of the term.
Similarly, one paper used the term to refer to a phenomenon whereby “public buyers decide to use restricted auctions to tender small contracts”, a practice which the researchers stated is “widespread among public buyers in EU member states”.
Finally, an associated concept is the strong law of small numbers, which is the adage that “There aren’t enough small numbers to meet the many demands made of them”. As described in the paper that popularized the concept:
“In examining cases involving small numbers a striking pattern may be encountered that strongly implies a general theorem. It is this implication Guy [mathematician Richard Guy] calls the strong law of small numbers. Sometimes the law works, sometimes it does not. If the pattern is no more than a set of coincidences, as it often is, a mathematician can waste an enormous amount of time trying to prove a false theorem. The law can also mislead in an opposite way. A few counterexamples may cause the mathematician to prematurely abandon a search for a theorem that is actually true but slightly more complicated than expected.”
— From “Mathematical Games: Patterns in primes are a clue to the strong law of small numbers” (in Scientific American, by Martin Gardener, 1980)
Richard Guy also published an associated 1988 article on the topic, and in 1990 he published an article on the second law strong law of small numbers, which is the adage that “When two numbers look equal, it ain’t necessarily so!”.
Summary and conclusions
- The law of small numbers (LOSN) is the incorrect belief that small samples are likely to be highly representative of the populations they come from (similarly to large samples).
- For example, the LOSN could cause someone to assume that the way one person behaves necessarily represents the way everyone from that person’s country behaves.
- This bias revolves around people’s expectation that the characteristics of a parent population will be represented locally in all of its parts.
- This bias can influence both people’s perception of how representative current samples are and their prediction of what samples will look like.
- To reduce this bias in yourself and others, you should identify situations where it might occur, question related reasoning (e.g., “is this sample big enough to be representative?”), illustrate the issues with it using examples, and use general debiasing techniques (like slowing down the reasoning process).