
Parsimony is a guiding principle which suggests that we should prefer simpler explanations and solutions over more complex ones, all other things being equal. For example, if you hear barking from inside your house, and you own a dog, it’s better to assume that you’re hearing your own dog right now, than to assume that another dog snuck in, unless you have a compelling reason to think otherwise.
In philosophical and scientific contexts, parsimony is also called the principle of parsimony or law of parsimony. In more general contexts, parsimony sometimes refers to reluctance to spend resources (especially money).
Parsimony can help guide your reasoning and decision-making in various scenarios, so it’s useful to understand it. As such, in the following article you will learn more about parsimony, and see how you can use it yourself as effectively as possible.
Examples of parsimony
An example of parsimony is that, if the lights in your room go out after you flip the light switch, you should generally prefer a simple explanation for this—that they went out because you flipped the switch—over more complex explanations, such as that there was a power outage at the exact moment you flipped the switch.
Parsimony also plays a role in scientific research. For example, when it comes to phylogenetic trees, which show potential relations between biological entities like individuals or species, the principle of maximum parsimony suggests that the preferred tree should be the one that can explain the relation through the smallest number of evolutionary changes.
In statistics and machine learning, parsimony means, for example, that if two models can explain the data equally well or above a certain threshold, then the one that contains fewer parameters should be preferred. Accordingly, parsimony often plays a role in model selection, for example in methods like Akaike information criterion (AIC), Bayesian information criterion (BIC), and regularized regression (e.g., lasso).
In addition, parsimony can also apply to solutions, rather than explanations. For example, parsimony means that if two machines can be used to do the same thing, you should prefer the machine that’s simpler to operate or maintain. Likewise, if you’re writing code and can choose between two approaches to achieve the same thing, you should prefer the one that’s simpler to write, maintain, and explain, all else being equal.
The preference for parsimony—which is sometimes also referred to as simplicity, elegance, or sparsity—has been expressed in many contexts. For instance, the following is an example of this in the context of developing scientific theories:
“In general, we consider it a good principle to explain the phenomena by the simplest hypotheses possible, in so far as there is nothing in the observations to provide a significant objection to such a procedure.”
— From “Almagest” (by astronomer Ptolemy, circa 150 CE)
The following is an example of this in the context of creating optimal algorithms:
“Simplicity. The key to performance is elegance, not battalions of special cases. The terrible temptation to tweak should be resisted unless the payoff is really noticeable.”
— From “Engineering a sort function” (by Jon Bentley and Douglas McIlroy, 1993)
Parsimony and Occam’s razor
Occam’s razor is a philosophical razor, which is meant to help identify the most likely explanations for phenomena. It denotes that, all things being equal, explanations that involve fewer assumptions should be preferred over ones that involve more assumptions.
Occam’s razor has been formulated in various ways over time, leading to some differences in how it’s applied. Two popular modern versions of it are “The simplest explanation is usually the best one” and “Shave away all but what is necessary”.
Occam’s razor is sometimes called the principle of parsimony, since it involves a preference for simpler explanations. However, two distinctions can be drawn between these concepts, depending on how exactly they’re formulated:
- Parsimony can be considered as a broad concept, which applies not only to explanations but also to solutions. Under this view, Occam’s razor can be considered a common tool for implementing the principle of parsimony in a specific way.
- Occam’s razor can be considered as focusing on a specific type of simplicity (fewer assumptions), while parsimony might also involve other forms of simplicity (e.g., less complex assumptions). This view is mainly based on earlier formulations of Occam’s razor, including “plurality should not be posited without necessity” (or “do not multiply entities without necessity”), and “it is useless to do with more what can be done with fewer”.
Benefits of parsimony
There are several potential benefits to explanation and solutions that are more parsimonious:
- Greater generalizability, for example when a certain solution is simple enough that it can be easily applied in many contexts.
- Higher interpretability and explainability, for example when parameters in a statistical model are easier to understand because there are fewer interactions between them and other parameters.
- Better operability and maintainability, for example when a machine is easier to use and keep functional because it has fewer moving parts.
- Fewer opportunities to make mistakes, for example because a procedure has fewer steps that can go wrong.
- Greater efficiency, for example because a simpler machine requires less work in order to activate and operate.
These tradeoffs aren’t always clear. For example, more parsimonious code might require more work upfront, but will save work over time because it’s easier to maintain.
In addition, a key purpose of parsimony is to serve as a counterbalancing force against the tendency to overfit explanations and solutions to specific circumstances. An example of this is shown in the following graphs, which illustrate how considering parsimony can lead to models (the lines) that better explain observations (the dots):
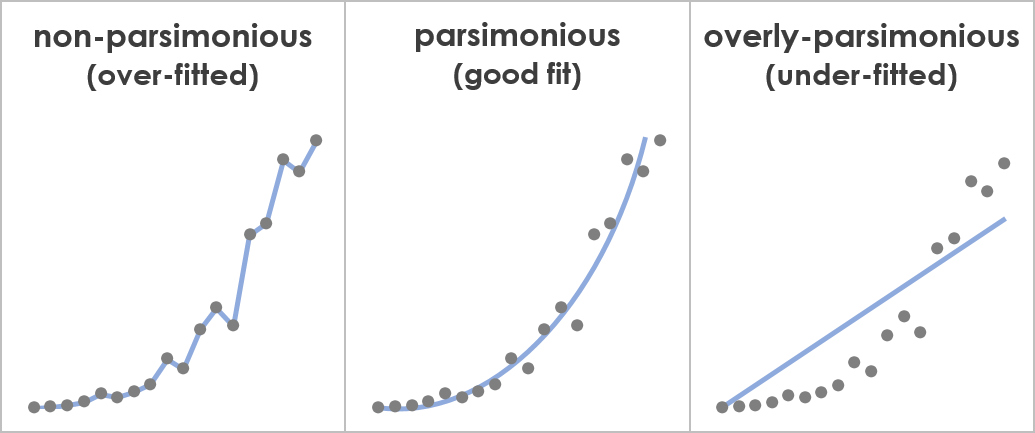
The left graph shows a non-parsimonious explanation, which is overfitted to the particular data points that were included in this sample and to their associated noise, so it won’t properly capture the process that generated them, and won’t generalize well to other data from the same population (e.g., in terms of explaining or predicting new data points). The middle graph shows a parsimonious explanation, which is properly fitted to the data, so it’s able to capture the underlying data-generating process in a generalizable manner. The right shows an overly-parsimonious explanation, which is underfitted, so it’s overly simplistic and fails to properly capture the underlying data-generating process. This demonstrates not only the importance of considering parsimony, but also of considering additional factors, like the ability of a model to actually explain the observed data.
Parsimony can provide a similar benefit in various everyday situations. For example, preferring simpler explanations can help us avoid jumping to conclusions, in cases where we are prone to see patterns in noise or connections between unrelated things (a phenomenon called apophenia). In addition, parsimony can help us avoid unnecessarily complex explanations for phenomena we encounter, which are often wrong and don’t generalize well outside the specific situation we’re in. These ad hoc hypotheses can be particularly problematic in certain cases, such as when confirmation bias drives us to interpret evidence in a way that supports our preexisting beliefs, rather than in a way that explains the evidence well.
For instance, consider a situation where you flip the light switch, after which the lights go out. You can come up with many explanations for why the lights went out, like:
- Because you flipped the switch.
- Because at the exact moment you flipped the switch, there was a power outage.
- Because at the exact moment you flipped the switch, you developed a special vision impairment that makes you think the lights went out.
- Because there’s an invisible alien in your room who shot a darkness field around the lights when you flipped the switch.
Here, parsimony would drive you to accept the simplest explanation, rather than come up with an infinite number of complex explanations. This is especially important when these alternative explanations are costly to test (e.g., in terms of time and effort), or are entirely impossible to confirm or falsify.
Caveats about parsimony
Despite the potential benefits of considering parsimony, this principle should be used with caution, since it can cause some issues. Most notably, parsimony is only one of several factors to consider, and often has tradeoff with other factors, like the ability to explain observations. In addition, parsimony doesn’t guarantee the correctness of explanations or the optimality of solutions, despite misconceptions to the contrary.
Below is further information about these caveats, as well as about additional caveats about and criticisms of parsimony.
Parsimony is one of several factors to consider
Although parsimony can be a useful factor to consider when choosing between multiple explanations or solutions, it’s only one of several factors to consider. For example:
- If one explanation is slightly more complex than another, but is far better able to explain a certain phenomenon, then it might be preferable to prefer the more complex explanation, even though it’s less parsimonious.
- If you need to choose between several possible approaches for writing a piece of code, parsimony is only one factor to consider, alongside factors like how well the code will work and how easy it will be to maintain it.
- If a statistical model contains many parameters that don’t predict the data, sharing this non-parsimonious model may be worthwhile, in cases where the lack of predictive ability of those parameters is a novel insight.
Essentially, the important thing to understand is that parsimony doesn’t mean that you should always pick the simplest explanation or solution. Rather, it means that you should consider simplicity as an important factor, alongside other relevant factors, like the ability of a theory to actually explain the phenomenon that it’s meant to explain. In other words, although parsimony is beneficial, it must be tempered by other considerations, like explanatory power.
This is expressed, for example, in the Chatton Principle, which is the adage that:
“Consider an affirmative proposition, which, when it is verified, is verified only for things; if three things do not suffice for the purpose of verifying it, one has to posit a fourth, and so on in turn.”
Likewise, physicist Albert Einstein said that:
“It can scarcely be denied that the supreme goal of all theory is to make the irreducible basic elements as simple and as few as possible without having to surrender the adequate representation of a single datum of experience.”
This has been re-formulated as Einstein’s razor, which states that:
“Things should be made as simple as possible, but not simpler.”
Note: Principles that oppose (or seem to oppose) parsimony are sometimes called anti-razors or counter-razors, in reference to Occam’s razor as a popular way to implement parsimony. However, these principles can also be considered philosophical razors, since they’re meant to help find the most likely explanation for phenomena, and they don’t necessarily contradict Occam’s razor, some of whose formulations acknowledge the possible necessity of complex explanations.
Parsimony can involve tradeoffs
Increased parsimony of explanations and solutions often comes at the expense of other important considerations. For example, more parsimonious statistical models can have lower explanatory power and worse goodness-of-fit to observed data, so while parsimony can help avoid overfitting, it can cause underfitting instead (which relates to the well-known bias-variance tradeoff). Similarly, a simpler mechanical solution might be easier to implement and maintain, but also less effective than a more complex solution, when it comes to handling important edge cases.
Whether a tradeoff between parsimony and another factor is worthwhile depends on factors like your circumstances and goals. For example, you might care about parsimony to a different extent when considering the likelihood that a certain model reflects an underlying phenomenon than when using a model for predictive purposes.
Parsimony doesn’t guarantee correctness or optimality
Although parsimony can help select a preferred explanation or solution, parsimonious explanations can be wrong, and parsimonious solutions can be worse than potential alternatives.
For example, in medicine, diagnostic parsimony guides physicians to assume that if a patient is displaying multiple symptoms, then those symptoms should be attributed to a single medical condition. However, this assumption can be false, as noted in Hickam’s dictum, which is the adage that “patients can have as many diseases as they damn well please”.
Likewise, a related concept in diagnostic medicine is the zebra principle, which states that “when you hear hoofbeats, think of horses, not zebras”. This denotes that if a patient’s symptoms could equally fit either a relatively common medical condition (a “horse”) or a rare condition (a “zebra”), then the more common condition is more likely. However, this principle doesn’t mean that patients necessarily suffer from the more common condition, as some can suffer from the rarer condition instead.
This caveat plays a role in many other contexts, since reality is often complex, and can therefore necessitate complex explanations and solutions. This is expressed, for example, in H. L. Mencken’s adage that:
“…there is always a well-known solution to every human problem—neat, plausible, and wrong.”
Note: Parsimony is a form of abductive reasoning, which leads to conclusions that are likely true, as opposed to deductive reasoning, which leads to conclusions that are necessarily true (if the reasoning is logically sound). When used in practical situations, parsimony often serves as a heuristic, meaning that it’s a mental shortcut that’s meant to help people make decisions quickly and efficiently.
Parsimony can mean many things
The concept of parsimony can vary based on things like who’s discussing it, what context it’s being discussed in (e.g., in different academic fields), what the parsimony is applied to (e.g., statistical models, scientific hypotheses, or mechanical solutions), what type of parsimony is being considered (e.g., parsimony that is quantitative vs. qualitative), and what the focus of the discussion on parsimony is (e.g., considerations that are aesthetic, ontological, epistemological). Furthermore, various distinctions are sometimes drawn between parsimony and related concepts (e.g., between parsimony as a form of ontological simplicity and elegance as a form of syntactic simplicity). All this adds complexity to discussions and criticisms of this phenomenon, as there are many different interpretations of what “parsimony” means exactly, and different interpretations can involve different potential benefits and problems.
Many of these distinctions are mainly relevant to theoretical discussions of this phenomenon, but some also have practical implications. For example, if one explanation involves fewer assumptions than another, but these assumptions are ones with a lower likelihood of being true, then it might be unclear which explanation is simpler overall. Likewise, if one solution (e.g., machine or programmatic code) is simpler to use, another is simpler to maintain, and another is simpler to explain, it might be unclear which solution is simpler overall.
How to apply parsimony
To use the concept of parsimony in practice, you should prefer simpler explanations or solutions over complex ones, all other things being equal. If things aren’t equal, then you should consider parsimony as one relevant factor, and weigh it against other factors that matter in your case, like the ability to explain observed data.
When using parsimony in this manner, you should use your judgment and consider all its potential benefits, but also the important caveats about it, which are outlined above. Most notably, remember that parsimony can involve tradeoffs with other factors, and that it doesn’t guarantee the correctness of explanations or the optimality of solutions.
Summary and conclusions
- Parsimony is a guiding principle, which suggests that we should prefer simpler explanations and solutions over more complex ones, all other things being equal.
- For example, if you hear barking from inside your house, and you own a dog, it’s better to assume that you’re hearing your own dog right now, than to assume that another dog snuck in, unless you have a compelling reason to think otherwise.
- Parsimony serves as a counterbalancing force against the tendency to overfit explanations and solutions to very specific circumstances, and has various benefits, like greater generalizability of explanations and solutions across different circumstances.
- Parsimony is only one of several factors to consider, and it often involves tradeoffs with other factors, like the ability to explain specific observations.
- Parsimony doesn’t guarantee correctness of explanations or optimality of solutions, and the concept of parsimony is sometimes interpreted in different ways by different people under different circumstances.